Ray Tracing From Scratch in Python
Create a computer-generated image using the Ray Tracing algorithm coded from scratch in Python.

In this post I will give you a glimpse of what computer graphics algorithms may look like. I will explain the ray tracing algorithm and show a simple implementation in Python.
By the end of this article you’ll be able to make a program that will generate the above image, without making use of any fancy graphic library! Only NumPy. Isn’t it crazy?! Let’s dive in!
P.S. This article is by no mean a complete guide / explanation of ray tracing, since this is such a vast subject, but rather an introduction for curious people :)
Prerequisites
We only need very basic vector geometry.
- If you have 2 points A and B — whatever the dimensionality: 1, 2, 3, …, n — then a vector that goes from
AtoBcan be found by computingB — A(element-wise); - The length of a vector — whatever the dimensionality — can be found by computing the square root of the sum of the squared components. The length of a vector
vis denoted||v||; - A unit-vector is a vector of length 1:
||v|| = 1; - Given a vector, another vector that points to the same direction but with a length of 1 can be found by dividing each component of the first vector by its length — this is called normalization:
u = v / ||v||; - Dot product for vectors. Specifically:
<v, v> = ||v||²; - Solving a quadratic equation;
- A bit of patience and imagination;
Ray Tracing Algorithm
In effect, ray tracing is a rendering technique that simulates the path of light and intersections with objects and is able to produce images with a high degree of realism. More optimized variations of this algorithm are actually used in video games!
To explain the algorithm we need to setup a scene:
- We need a 3D space (that simply means we’re going to use 3 coordinates to position objects in space);
- We need objects in that space (since we’re going to reproduce
fig. 1, imagine spheres); - We need a source of light (this is going to be a single point emitting light in all directions, so in essence a single position);
- We need an “eye” or a camera to observe the scene (again, simply a position);
- Since the camera could be looking anywhere really, we need a screen through which the camera will be observing the objects (4 positions for the four corners of a rectangular screen);

A word about the screen: the screen is going to occupy a certain amount of space that you will define (could be a 3x2 rectangle for instance). But 3 and 2 don’t really mean anything alone. They do mean something when you compare them to the sizes of other objects, they are relative. What’s important here, is how you will split that rectangle into smaller squares (pixels), akin the figure above. This is going to determine the size of the final image. In other words, you can create a 3x2 rectangle and split it into 300x200 pixels, that will work just fine.
Given the scene, this is the ray tracing algorithm:
for each pixel p(x,y,z) of the screen:
associate a black color to p
if the ray (line) that starts at camera and goes towards p intersects any object of the scene then:
calculate the intersection point to the nearest object
if there is no object of the scene in-between the intersection point and the light then:
calculate the color of the intersection point
associate the color of the intersection point to p
Note that this process is actually the reverse process of real-life illumination. In reality, light comes out of the source in all directions, bounce on objects and hits your eye. However, since not all rays coming out the light source will end up in your eye, ray tracing does the reverse process to save computation time (trace rays from the eye back to the light source).
This is all purely geometrical, the only thing I didn’t explain is how to calculate the color of the intersection point. This is isn’t necessary right now, so I will explain it later. Just know there exist physical models that describe how objects are illuminated when light strikes on them with a certain angle, intensity, etc.
At the end of the algorithm we will have filled the screen with the correct colors, and we can just save it as an image.
Setup the scene
Before starting to code, we need to setup a scene. For now we will decide where the camera and the screen are located. For our purpose, we will make things simple by aligning them with the unit axes.

Hence, the camera is located at the point (x=0, y=0, z=1) and the screen is part of the plane formed by the x and y axes. With that being set up, we can already write the skeleton of our code.
- The camera is just a position, 3 coordinates;
- The screen on the other hand is defined by four numbers (or two points): left, top, right, bottom. It ranges from
-1to1in the x direction (this is arbitrary), and ranges from-1 / ratioto1 / ratioin the y direction, where ratio isimage width / image height. The reason for this is simple: we want the screen to have the same aspect ratio than the actual image we want to produce. Setting up the screen this way will produce an aspect ratio of (width over height):2 / (2 / ratio) = ratiowhich is the ratio of the desired image of300x200; - Finally, the loop consists of splitting the screen into
widthandheightpoints in the x and y directions respectively, then computing the color of the current pixel;
You can actually run that code and it will produce — as expected for now — a black image. If you look back at the pseudo-code then this is what we accomplished.
✅ for each pixel p(x,y,z) of the screen:
✅ associate a black color to p
if the ray (line) that starts at camera and goes towards p intersects any object of the scene then:
calculate the intersection point to the nearest object
if there is no object of the scene in-between the intersection point and the light then:
calculate the color of the intersection point
associate the color of the intersection point to pRay intersection
The next step of the algorithm is: if the ray (line) that starts at camera and goes towards p intersects any object of the scene then.
Let’s break it down into two parts. First, what is the ray (line) that starts at camera and goes towards p ?
Ray definition
We say “ray” but that’s really just another word for “line”. In general, whenever you code something that is geometrical, you should prefer vectors over actual line equations, they really are easier to work with and are much less prone to errors such as division by zero.
So, since the ray starts at the camera and goes in the direction of the currently targeted pixel, we can define a unit-vector that points to a similar direction. Therefore, we define a “ray that starts at camera and goes towards pixel” as the following equation:
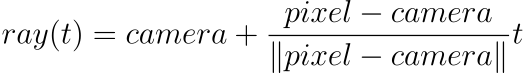
Remember, camera and pixel are 3D-points. For t=0 you end up at the camera position, and the more you increase t the further away you get from the camera in the direction of the pixel. This is a parametric equation, that yields a point along the line for a given t.
Of course, there is nothing special about camera or pixel, we can similarly define a ray that starts at origin (O) and goes towards destination (D) as:
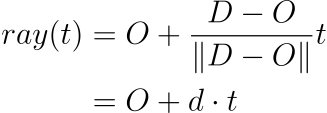
For convenience, we define d as the direction vector.
We can now complete the code and add the computation of the ray.
- We’ve added the
normalize(vector)function that returns a… normalized vector; - We’ve added the computation of
originanddirectionwhich both together define a ray. Notice that pixel hasz=0since it lies on the screen which is contained in the plane formed by the x and y axes;
Now we get to the second part which is intersects any object of the scene then. That is basically the “hard” part. The computation is going to be different for each type of objects we will dealing with (spheres, planes, triangles, etc.). For the sake of simplicity, we will only render spheres. So for the next part we will see:
- How we define a sphere;
- How we compute the intersection point between a ray and a sphere, if it exists;
Sphere definition
A sphere is actually a pretty simple mathematical object to define. A sphere is defined as the set of points that are all at the same distance r (radius) from a given point (center).
Therefore, given the center C of a sphere, and its radius r, an arbitrary point X lies on the sphere if and only if:
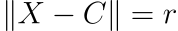
For convenience, we square both sides to get rid of the square root caused by the magnitude of X — C.
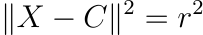
We can already define some spheres just after the screen declaration.
Now let’s compute the intersection between a ray and a sphere.
Sphere Intersection
We know the ray equation, and we know what condition a point must satisfy so that it lays on a sphere. All we have to do is plug eq. 2 into eq. 4 and solve for t. Which means, answering the question: for which t, ray(t) will be on the sphere ?
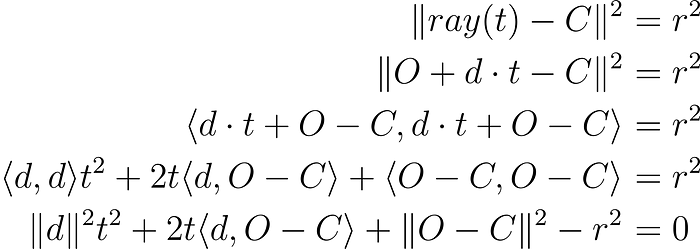
This is an ordinary quadratic equation that we can solve for t. We will call the coefficients associated with t², t¹, t⁰ a, b, and c respectively. Let’s calculate the discriminant of that equation:
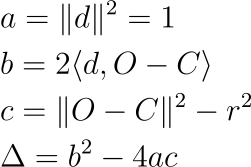
Since d (direction) is a unit-vector, we have a=1. Once we calculate the discriminant of that equation, there are 3 possibilities:

We will only use the third case to detect intersections. Here’s a function that can detect intersections between a ray and a sphere. It will return t the distance from the origin of the ray to the nearest intersection point if the ray actually intersects the sphere, and it will return None otherwise.
Notice that we only return the nearest intersection (because there are 2) only when both t1 and t2 are positive. This is because a t that solves the equation could be negative, but it would mean that the ray that intersects the sphere doesn’t have d as a direction vector, but -d (for instance if the sphere is behind the camera and the screen).
Nearest intersected object
All right, so far so good, but we still haven’t completed the instruction from the pseudo-code which was: if the ray (line) that starts at camera and goes towards p intersects any object of the scene then[...]. Good news is, we can do this and the next instruction in one strike! The next instruction is: calculate the intersection point to the nearest object.
We can easily create a function that uses sphere_intersect() to find the nearest object that a ray intersects, if it exists. We simply loop over all the spheres, search for intersections, and keep the nearest sphere.
When calling the function, if nearest_object is None then there is no object intersected by the ray, otherwise its value is the nearest intersected object and we get min_distance, the distance from the ray origin to the intersection point.
Intersection point
In order to compute the intersection point, we use the previous function:
nearest_object, distance = nearest_intersected_object(objects, o, d)
if nearest_object:
intersection_point = o + d * distanceHooray! We’ve completed the second and the third instructions. This is the code we have until now:
✅ for each pixel p(x,y,z) of the screen:
✅ associate a black color to p
✅ if the ray (line) that starts at camera and goes towards p intersects any object of the scene then:
✅ calculate the intersection point to the nearest object
if there is no object of the scene in-between the intersection point and the light then:
calculate the color of the intersection point
associate the color of the intersection point to pLight intersection
So far, we know if there is a straight line that goes from the camera/eye to an object, and we know which object this is, as well as exactly what part of the object we’re looking at. What we don’t know yet is if that specific point is illuminated at all! Maybe the light isn’t striking on that particular point, and so there is no need to go further because we cannot see it. Therefore, the next step is to check if there is no object of the scene in-between the intersection point and the light.
Fortunately, we already have a function to help us: nearest_intersected_object(). Indeed, we want to know if the ray that starts at the intersection point and goes towards the light is intersecting an object of the scene before crossing the light. This is practically the same task as previously, we just need to change the ray origin and direction. First, we need to define a light. You can add this near the objects declaration:
light = { 'position': np.array([5, 5, 5]) }To check if an object is shadowing the intersection point, we have to pass the ray that starts at the intersection point and goes towards the light, and see if the nearest object returned is actually closer than the light to the intersection point (in other words, in between).
Looks neat, doesn’t it ? Well this is not going to work… We need to make a slight adjustment. If we use the intersection point as the origin of the new ray we might end up detecting the sphere where we currently stand as an object in between the intersection point and the light. A quick and widely used fix for that problem is to take a little step that gets us away from the surface of the sphere. We generally use a normal vector to the surface and take a little step in that direction.

This trick isn’t used only for spheres, but for any kind object.
Therefore, the correct code is:
✅ for each pixel p(x,y,z) of the screen:
✅ associate a black color to p
✅ if the ray (line) that starts at camera and goes towards p intersects any object of the scene then:
✅ calculate the intersection point to the nearest object
✅ if there is no object of the scene in-between the intersection point and the light then:
calculate the color of the intersection point
associate the color of the intersection point to pBlinn-Phong reflection model
This is it, the last part. We know a light beam has stroke the object, and the reflection of the beam got straight into the camera. The question is: What does the camera see ? This is what the Blinn-Phong model attempts to answer.
FYI: The Blinn-Phong model is an approximation to the Phong model that is less computationally intensive.
According to this model, any material has 4 properties:
- Ambient color: color that an object is suppose to have in absence of light. It’s hard to imagine, since we only see objects when light strikes on them, but generally this is a dim color tinted with the actual color you imagine;
- Diffuse color: color that is the closest to what we think of when we say “color”;
- Specular color: color of the shiny part of an object when light has stroke on it. Most of the time this is white;
- Shininess: a coefficient representing how shiny an object is;
Note: All colors are RGB representations in the range 0–1.

So every object of the scene must have these 4 properties. Let’s add them to the spheres.
In this example, the spheres are red, magenta, and green respectively.
The Blinn-Phong model states that light also has the three color properties: ambient, diffuse and specular. Let’s add them too.
Given these properties, the Blinn-Phong model calculates the illumination of a point as follows:
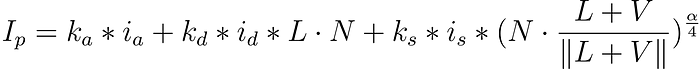
where,
ka,kd,ksare the ambient, diffuse, specular properties of the object;ia,id,isare the ambient, diffuse, specular properties of the light;Lis a direction unit vector from the intersection point towards the light;Nis the unit normal vector to the surface of the object at the intersection point;Vis a direction unit vector from the intersection point towards the camera;αis the shininess of the object;
Notice that at the end, we bound the color between 0 and 1 to make sure it’s in the correct range.
✅ for each pixel p(x,y,z) of the screen:
✅ associate a black color to p
✅ if the ray (line) that starts at camera and goes towards p intersects any object of the scene then:
✅ calculate the intersection point to the nearest object
✅ if there is no object of the scene in-between the intersection point and the light then:
✅ calculate the color of the intersection point
✅ associate the color of the intersection point to pRun the code!
Increase width and height for a higher resolution (at the cost of your time).

Wow that’s cool! However, you may notice 2 things that differ from the first image I’ve shown at the beginning. Go ahead, take a look back.
- The grey floor is missing;
- There are no reflections (mirror effect) in this picture;
Let’s address these two points.
Fake plane
Ideally we would create another type of object, a plane, but because we’re lazy we can simply use another sphere. How ? Well, if you’re standing on a sphere that has an infinitely large radius (compared to your size), then you’ll feel like you’re standing on a flat surface. Just like earth :)
Add this sphere to your list of objects, and render again!
{ 'center': np.array([0, -9000, 0]), 'radius': 9000 - 0.7, 'ambient': np.array([0.1, 0.1, 0.1]), 'diffuse': np.array([0.6, 0.6, 0.6]), 'specular': np.array([1, 1, 1]), 'shininess': 100 }Reflection
Right now, we render rays that: come out the light source, hit the surface of an object, then directly bounce towards the camera. What if the ray hits multiple objects before hitting the camera ? This is reflection. The ray will accumulate different colors and when it strikes the camera you will see reflections. Let’s do it.
Each object has a reflection coefficient in the range 0–1. “0” means the object is matte, “1” means the object is like a mirror. Let’s add a reflection property to all the spheres:
{ 'center': np.array([-0.2, 0, -1]), ..., 'reflection': 0.5 }
{ 'center': np.array([0.1, -0.3, 0]), ..., 'reflection': 0.5 }
{ 'center': np.array([-0.3, 0, 0]), ..., 'reflection': 0.5 }
{ 'center': np.array([0, -9000, 0]), ..., 'reflection': 0.5 }Algorithm
Currently, we compute a ray that starts at the camera and goes towards a pixel, then we trace that ray into the scene, check for the nearest intersection and compute the intersection point color.
In order to include reflections, we need to trace the reflected ray after an intersection happen and include the color contribution of each intersection point. We repeat that process some number of time (to define).

Color computation
In order to get the color of a pixel, we need to sum the contribution of each intersected point by the ray.
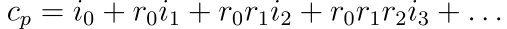
where,
cis the (final) color of a pixel;iis the illumination computed by the Blinn-Phong model of the #index intersection point;ris the reflection of the #index intersected object;
Then it’s up to you to decide when to stop computing that sum (i.e. when to stop tracing reflected rays).
Reflected ray
Before we’re able to code this, we need to find the reflected ray direction. We can compute a reflected ray the following way:
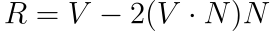

where,
- R is the normalized reflected ray;
- V is a direction unit vector of the ray to be reflected;
- N is the direction unit vector normal to the surface the ray stroke;
Add this method at the top of the file along with the normalize() function:
Code
Time to code this. It’s actually a small change at the end. Simply make the following changes:
Important: Now that we have put the intersection code in another loop for reflection, we should use break statements where we previously used continue statements, in order to avoid useless computations.
That’s it! Run the code and observe the beautiful result!

Final Code
The final code is surprisingly small, about a hundred lines of code!
What’s next ?
This was a very simplistic program that was meant to educate on the subject. There are so many ways to improve this and implement other fascinating functionalities. Here are some of them:
- OOP! Right now we’ve put all the objects in a dict, but you could make classes, figure out what’s specific to spheres and what’s not, make a base class, and implement other objects such as planes or triangles;
- Same thing goes for light. Add some POO here and make it so you can add multiple lights in the scene;
- Separate the material properties from the geometrical properties, to be able to apply one material (e.g. blue matte) to any type of objects;
- Figure out a way to position the screen correctly given any camera position and a direction to look at;
- Model the light differently. Currently it’s a single point, which is why the shadows of objects are “hard” or well defined. In order to get “soft” shadows (with a gradient basically), you need to model a light like a 2d or 3d object: disk or sphere?
Bonus
Here’s an animation I made with ray tracing. I simply rendered the scene several times with the camera at different positions.
The code is in Kotlin (you’ll notice then how much python is slow…) and available on GitHub if you’re interested.
Conclusion
Congratulation if you made so far! I hope you enjoyed this fascinating subject and don’t hesitate to comment for any question. For further readings on that matter I would highly advise the following website:
Cheers !
